Metodo di Eulero
 Disambiguazione – Se stai cercando l'omonimo metodo di fattorizzazione, vedi Metodo di fattorizzazione di Eulero.
Disambiguazione – Se stai cercando l'omonimo metodo di fattorizzazione, vedi Metodo di fattorizzazione di Eulero.In matematica e informatica, il metodo di Eulero è una procedura numerica del primo ordine per risolvere equazioni differenziali ordinarie (ODE) una volta fornito un valore iniziale. Si tratta del più basilare dei metodi espliciti per l'integrazione numerica di equazioni differenziali ordinarie, ed è il più semplice metodo Runge-Kutta. Prende il nome da Leonhard Euler, il quale lo espose nel suo libro Institutionum calculi integralis pubblicato nel 1768–70.
Introduzione
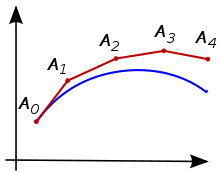
Si consideri il problema del calcolo della forma di una curva sconosciuta che inizia in un certo punto e soddisfa una data equazione differenziale. In questo caso, un'equazione differenziale ordinaria può essere immaginata come una formula tramite cui il coefficiente angolare della retta tangente alla curva può essere calcolato in ogni punto della curva. Si prenda quindi un piccolo incremento sulla retta tangente, da fino ad un punto sufficientemente vicino. Si può supporre che in questo intervallo il coefficiente angolare non cambi significativamente, quindi se si assume che è ancora sulla curva si può utilizzare nuovamente lo stesso ragionamento fatto per il punto in modo che, dopo diversi passi, viene generata una curva poligonale come mostrato nella figura a lato. Si tratta di una curva che non diverge troppo dalla curva originale sconosciuta; l'errore tra le due curve può essere diminuito se l'incremento è piccolo abbastanza e l'intervallo di calcolo è finito.
Formulazione
Si supponga di voler approssimare la soluzione del problema di Cauchy:
discretizzando la variabile , quindi definendo , con la dimensione di ogni intervallo. Tra e il comportamento della soluzione può essere approssimato stimando:
dove il valore di risulta essere un'approssimazione della soluzione della ODE al tempo . Il metodo di Eulero è esplicito, ovvero la soluzione è una funzione esplicita di per .
Il metodo integra una equazione differenziale ordinaria del primo ordine; tuttavia per un'equazione differenziale di ordine N:
si introducono le variabili ausiliari in modo da ottenere l'equazione equivalente:
Si tratta di un sistema del primo ordine nella variabile , e può essere approssimato col metodo di Eulero o con qualsiasi altro metodo per sistemi del primo ordine.
Esempio
Dato il valore iniziale del problema:
si vuole utilizzare il metodo di Eulero per approssimare .
Incremento h = 1

Il metodo di Eulero prevede:
Per calcolare , essendo la funzione definita da si ha:
Per ottenere il successivo valore da utilizzare nei calcoli:
e allo stesso modo con , e :
A causa della natura ripetitiva di questo algoritmo, può essere utile organizzare i calcoli sotto forma di grafico:
0 1 0 1 1 1 2 1 2 1 2 1 2 4 2 4 2 4 1 4 8 3 8 3 8 1 8 16
La conclusione di questo calcolo è . La soluzione esatta della equazione differenziale è , quindi : l'approssimazione del metodo di Eulero con non è buona in questo caso, sebbene il suo comportamento è qualitativamente corretto. Una stima migliore si ottiene riducendo .
Diversi valori per l'incremento

Il metodo di Eulero è maggiormente accurato al diminuire del passo ; la tabella sottostante mostra i diversi risultati sfruttando passi di diverse dimensioni. La prima riga corrisponde all'esempio della sezione precedente mentre la seconda riga è illustrata in figura:
passo risultato con Eulero errore 1 16 38,598 0,25 35,53 19,07 0,1 45,26 9,34 0,05 49,56 5,04 0,025 51,98 2,62 0,0125 53,26 1,34
L'errore riportato nell'ultima colonna della tabella indica la differenza tra la soluzione esatta per e l'approssimazione con il metodo di Eulero. Si può constatare che al dimezzarsi del passo corrisponde approssimativamente un dimezzamento dell'errore, questo suggerisce che l'errore è all'incirca proporzionale alla dimensione del passo, almeno per piccoli valori di . Questo è vero in generale ed anche per altre equazioni.
Altri metodi, come la regola del punto medio, sono generalmente più precisi: sfruttando il punto medio l'errore è all'incirca proporzionale al quadrato del passo. Per questo motivo il metodo di Eulero viene definito del primo ordine, mentre il metodo del punto medio del secondo ordine.
Dalla tabella è possibile affermare che il passo necessario per approssimare un risultato fino alla terza cifra decimale è circa 0.00001: il che significa che saranno necessari 400000 passi. Questo alto numero di passi implica un alto costo computazionale. Per questo motivo generalmente si preferiscono metodi numerici più precisi (cioè di ordine maggiore) come ad esempio il metodo di Runge-Kutta oppure i metodi lineari multistep, soprattutto se è necessaria grande accuratezza.
Derivazione ed errore di troncamento locale
Ci sono diversi modi per ricavare il metodo di Eulero; ad esempio si può considerare l'espansione di Taylor di intorno a :
e quindi sostituire ignorando i termini al quadrato e di ordine superiore. L'errore di troncamento locale che si ha con tale approssimazione è dato dalla differenza tra la soluzione :
e la soluzione al tempo fornita con il precedente sviluppo, ovvero:
dove la derivata terza di è supposta limitata. L'errore è quindi proporzionale, per piccoli , ad : l'estensione del metodo di Eulero, che si ha ad esempio con i metodi di Runge-Kutta, consente di avere stime più accurate, in cui l'errore è proporzionale a potenze maggiori di ,
Un'altra derivazione del metodo utilizza le differenze finite per scrivere la derivata:
in modo che sostituendo tale espressione in si ottiene il metodo di Eulero.
Si può infine integrare direttamente l'equazione differenziale tra e e applicare il teorema fondamentale del calcolo integrale:
Quindi si approssima l'integrale con la regola del rettangolo:
e combinando entrambe le equazioni si trova il metodo di Eulero.
Implementazione
Di seguito una possibile implementazione del metodo in linguaggio Matlab
function [th,uh]=eulero_avanti(f,t_0,t_max,y0,h) th=t_0:h:t_max; uh=zeros(length(th),1); uh(1)=y0; for i=1:length(th)-1 u_new = uh(i) + h*f(th(i),uh(i)); uh(i+1)=u_new; end end
Bibliografia
- (EN) Kendall A. Atkinson, An Introduction to Numerical Analysis, 2nd, New York, John Wiley & Sons, 1989, ISBN 978-0-471-50023-0.
- (EN) Uri M. Ascher e Linda R. Petzold, Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations, Philadelphia, Society for Industrial and Applied Mathematics, 1998, ISBN 978-0-89871-412-8.
- (EN) John C. Butcher, Numerical Methods for Ordinary Differential Equations, New York, John Wiley & Sons, 2003, ISBN 978-0-471-96758-3.
- (EN) Ernst Hairer, Syvert Paul Nørsett e Gerhard Wanner, Solving ordinary differential equations I: Nonstiff problems, Berlin, New York, Springer-Verlag, 1993, ISBN 978-3-540-56670-0.
- (EN) Arieh Iserles, A First Course in the Numerical Analysis of Differential Equations, Cambridge University Press, 1996, ISBN 978-0-521-55655-2.
- (EN) Josef Stoer e Roland Bulirsch, Introduction to Numerical Analysis, 3rd, Berlin, New York, Springer-Verlag, 2002, ISBN 978-0-387-95452-3.
- (EN) Taras I. Lakoba, Simple Euler method and its modifications (PDF) (Lecture notes for MATH334, University of Vermont), 2012. URL consultato il 29 febbraio 2012.
Voci correlate
- Integrazione numerica
- Metodi di Runge-Kutta
- Metodi di soluzione numerica per equazioni differenziali ordinarie
- Metodo di Eulero all'indietro
- Metodo di Eulero semi-implicito
- Problema di Cauchy
Altri progetti
Altri progetti
- Wikimedia Commons
 Wikimedia Commons contiene immagini o altri file su metodo di Eulero
Wikimedia Commons contiene immagini o altri file su metodo di Eulero
Collegamenti esterni
- (EN) Euler's Method for O.D.E.'sArchiviato il 16 luglio 2013 in Internet Archive., by John H. Matthews, California State University at Fullerton.
 Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica
Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica
































































