双代数

数学において，体 K 上の双代数（そうだいすう，英: bialgebra）とは，K 上のベクトル空間であって，単位的結合代数かつ余代数であるようなものである．代数構造と余代数構造はさらなる公理によって整合性を持つ．具体的には，余積と余単位はともに単位的代数の準同型である，あるいは同じことであるが，代数の積と単位射はともに余代数の準同型である．（これらのステートメントは同じ可換図式によって表されるから同値である．）

類似している双代数は双代数準同型によって関連付けられる．双代数の準同型は代数と余代数両方の準同型であるような線型写像である．

可換図式の対称性に反映されているように，双代数の定義は自己双対であり，したがって，B の双対を定義できるならば（B が有限次元ならいつでも可能である），自動的に双代数になる．

代数的構造
群に似た構造 群 半群 / モノイド 圭 準群とループ アーベル群 マグマ リー群 群論
環に似た構造 環 半環 近環（英語版） 可換環 整域 体 可除環 リー環 環論
束に似た構造 束 半束 可補束 全順序 ハイティング代数 ブール代数 en:Map of lattices 束論
加群に似た構造 加群 作用を持つ群 ベクトル空間 線形代数
代数に似た構造 代数 結合 非結合 合成代数 リー代数 次数付き 双代数 ホップ代数
表 話 編 歴

形式的な定義

(B, ∇, η, Δ, ε) が K 上の双代数 (bialgebra) であるとは，以下の性質を満たすことをいう：

• B は K 上のベクトル空間である；
• 2つの K 線型写像（乗法）∇: B ⊗ B → B（K 双線型写像 ∇: B × B → B と同値である）と（単位射）η: K → B が存在して，(B, ∇, η) は単位的結合的代数である；
• 2つの K 線型写像（余積）Δ: B → B ⊗ B と（余単位射）ε: B → K が存在して，(B, Δ, ε) は（余単位的余結合的）余代数である；
• 以下の可換図式によって表される協調性条件：

1. 乗法 ∇ と余乗法 Δ^[1]

   

   ただし τ: B ⊗ B → B ⊗ B は B のすべての x と y に対して τ(x ⊗ y) = y ⊗ x で定義される線型写像，

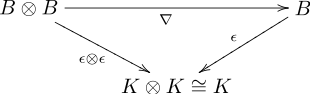
2. 乗法 ∇ と余単位 ε

   

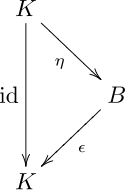
3. 余乗法 Δ と単位 η^[2]

   

4. 単位射 η と余単位射 ε

   

余結合性と余単位

K 線型写像 Δ: B → B ⊗ B が余結合的とは ${\displaystyle (\mathrm {id} _{B}\otimes \Delta )\circ \Delta =(\Delta \otimes \mathrm {id} _{B})\circ \Delta }$ が成り立つことをいう．

K 線型写像 ε: B → K が余単位射であるとは ${\displaystyle (\mathrm {id} _{B}\otimes \epsilon )\circ \Delta =\mathrm {id} _{B}=(\epsilon \otimes \mathrm {id} _{B})\circ \Delta }$ が成り立つことをいう．

余結合性と余単位射は次の2つの図式の可換性によって表される（それらは代数の結合性と単位元をあらわす図式の双対である）：

協調性の条件

4つの可換図式は「余積と余単位は代数の準同型である」あるいは同じことだが「積と単位射は余代数の準同型である」と読むことができる．

これらの主張は B の他の関係するすべてのベクトル空間における代数と余代数の自然な構造を説明すれば意味が分かる：(K, ∇₀, η₀) は明らかな方法で単位的結合代数であり，(B ⊗ B, ∇₂, η₂) は単位的結合代数で，単位射と積は

${\displaystyle \eta _{2}:=(\eta \otimes \eta ):K\otimes K\equiv K\to (B\otimes B)}$

${\displaystyle \nabla _{2}:=(\nabla \otimes \nabla )\circ (id\otimes \tau \otimes id):(B\otimes B)\otimes (B\otimes B)\to (B\otimes B)}$,

したがって ${\displaystyle \nabla _{2}((x_{1}\otimes x_{2})\otimes (y_{1}\otimes y_{2}))=\nabla (x_{1}\otimes y_{1})\otimes \nabla (x_{2}\otimes y_{2})}$ あるいは ∇ を省いて積を並置で書いて ${\displaystyle (x_{1}\otimes x_{2})(y_{1}\otimes y_{2})=x_{1}y_{1}\otimes x_{2}y_{2}}$;

同様に，(K, Δ₀, ε₀) は明らかな方法で余代数であり，B ⊗ B は余代数で余単位と余積は

${\displaystyle \epsilon _{2}:=(\epsilon \otimes \epsilon ):(B\otimes B)\to K\otimes K\equiv K}$

${\displaystyle \Delta _{2}:=(id\otimes \tau \otimes id)\circ (\Delta \otimes \Delta ):(B\otimes B)\to (B\otimes B)\otimes (B\otimes B)}$

である．

すると，図式 1 と 3 は Δ: B → B ⊗ B は単位的（結合）代数 (B, ∇, η) と (B ⊗ B, ∇₂, η₂) の準同型である

${\displaystyle \Delta \circ \nabla =\nabla _{2}\circ (\Delta \otimes \Delta ):(B\otimes B)\to (B\otimes B)}$, あるいは単に Δ(xy) = Δ(x) Δ(y),

${\displaystyle \Delta \circ \eta =\eta _{2}:K\to (B\otimes B)}$, あるいは単に Δ(1_B) = 1_{B ⊗ B}

と言っている；図式 2 と 4 は ε: B → K が単位的（結合）代数 (B, ∇, η) と (K, ∇₀, η₀) の準同型であると言っている：

${\displaystyle \epsilon \circ \nabla =\nabla _{0}\circ (\epsilon \otimes \epsilon ):(B\otimes B)\to K}$, あるいは単に ε(xy) = ε(x) ε(y)

${\displaystyle \epsilon \circ \eta =\eta _{0}:K\to K}$, あるいは単に ε(1_B) = 1_K.

同じことだが，図式 1 と 2 は ∇: B ⊗ B → B が（余単位的余結合）余代数 (B ⊗ B, Δ₂, ε₂) と (B, Δ, ε) の準同型である：

${\displaystyle \nabla \otimes \nabla \circ \Delta _{2}=\Delta \circ \nabla :(B\otimes B)\to (B\otimes B),}$

${\displaystyle \nabla _{0}\circ \epsilon _{2}=\epsilon \circ \nabla :(B\otimes B)\to K}$

と言っていて，図式 3 と 4 は η: K → B は（余単位的余結合）余代数 (K, Δ₀, ε₀) と (B, Δ, ε) の準同型である：

${\displaystyle \eta _{2}\circ \Delta _{0}=\Delta \circ \eta :K\to (B\otimes B),}$

${\displaystyle \eta _{0}\circ \epsilon _{0}=\epsilon \circ \eta :K\to K}$

と言っている．

例

群環

双代数の1つの例は，群 G から R への関数全体の集合であり，各 g ∈ G に対する標準基底ベクトル e_g の線型結合からなるベクトル空間 R^G として表すことができ，係数がすべて非負で和が 1 のときには G 上の確率分布を表している．余単位的余代数を生じる適切な余積と余単位の例は

${\displaystyle \Delta (\mathbf {e} _{g})=\mathbf {e} _{g}\otimes \mathbf {e} _{g},\quad \varepsilon (\mathbf {e} _{g})=1}$

であり（R^G 全体には線型性で伸ばす），余積は確率変数のコピーを作ることを表し，余単位は確率変数を「探知する」ことを表す，つまり，（単一のテンソル因子で表される）確率変数の値は忘れて残りの変数上の周辺分布（残りのテンソル因子）を得る．上のような確率変数のことばでの (Δ, ε) の解釈が与えられると，双代数の一貫性の条件は以下のような (∇, η) の制約条件に相当する：

1. η はすべてのほかの確率変数とは独立な正規化された確率分布を準備する作用素で，
2. 積 ∇ は2変数の確率分布を1変数の確率分布に写し，
3. η によって与えられる分布における確率変数をコピーすることは分布 η における2つの独立な確率変数を持つことと同値で，
4. 2つの確率変数の積を取ることと得られる確率変数のコピーを準備することは各確率変数のコピーを互いに独立に準備し対で一緒に掛けるのと同じ分布を持つ．

これらの制約を満たす対 (∇, η) は畳み込み作用素

${\displaystyle \nabla {\bigl (}\mathbf {e} _{g}\otimes \mathbf {e} _{h}{\bigr )}=\mathbf {e} _{gh}}$

である；これは2つの確率変数の分布から正規化された確率分布を生み出し，単位元としてデルタ分布 ${\displaystyle \eta =\mathbf {e} _{i}}$ を持つ，ただし i ∈ G は群 G の単位元を表す．

他の例

双代数の他の例にはテンソル代数があり，これは適切な余積と余単位を加えることで双代数にできる．詳細はその記事を参照のこと．

双代数は適切な対合射が見つけられればしばしばホップ代数に拡張できる．したがって，すべてのホップ代数は双代数の例である^[3]．積と余積の間に異なる両立性を持つ，あるいは異なるタイプの積と余積を持つ類似の構造には，リー双代数（英語版）やフロベニウス代数だある．さらなる例は余代数（英語版）の記事で与えられる．

関連項目

• 準双代数（英語版）
• フロベニウス代数
• ホップ代数

脚注

参考文献

• Dăscălescu, Sorin; Năstăsescu, Constantin; Raianu, Șerban (2001), Hopf Algebras: An introduction, Pure and Applied Mathematics, 235 (1st ed.), Marcel Dekker, ISBN 0-8247-0481-9 .